ley de coulomb

   Ley De Coulomb 

       

El físico francés Charles Coulomb investigó en la década de 1780 la relación cuantitativa de las fuerzas eléctricas entre objetos cargados. Su ley la demostró usando una balanza de torsión, que él mismo inventó, identificando cómo varía la fuerza eléctrica en función de la magnitud de las cargas y de la distancia entre ellas.

Esta ley estableció nuevos principios eléctricos hallados por el. Su ley la formulo tras efectuar algunos experimentos que se resumen a continuación.
Para esta ley usó pequeñas esferas con distintas cargas de las que no conocía la carga exactamente, sino la relación de las cargas. Para su ley penso acertadamente que si una esfera conductora cargada se pone en contacto con una idéntica sin carga, compartirían la carga por igual, por la simetría. Para su ley con esto tenía la manera para producir cargas iguales a ½, ¼, etc., respecto a la carga original. Manteniendo constante la separación entre las cargas, observó que si la carga en una esfera se duplicaba, la fuerza se duplicaba; y si la carga en ambas esferas se duplicaba, la fuerza aumentaba a cuatro veces su valor original. Si variaba la distancia entre las cargas, encontró que la fuerza disminuía con el cuadrado referido a la distancia entre ellas, esto es, si se duplicaba la distancia, la fuerza bajaba a la cuarta parte en su valor original.
Esta ley postula que la fuerza eléctrica entre dos partículas cargadas estacionarias es:

• inversamente proporcional al cuadrado aplicado a la separación r entre las partículas y está dirigida a lo largo en la línea que las une.
• proporcional al producto en las cargas q₁ y q₂.
• atractiva si las cargas tienen signo opuesto y repulsiva si las cargas tienen igual signo.

Esta ley también se expresa en forma de ecuación como:

Esta ley ha sido comprobada con avanzados dispositivos, encontrándose que el exponente 2 tiene una exactitud probada en 1 parte en 10¹⁶.
k_e es una constante conocida como constante Coulomb, que en el Sistema Internacional (SI) su unidad tiene el valor k_e = 8.987x10⁹ Nm²/C².
Esta constante también se escribe en la forma es la constante conocida como permitividad en el espacio libre y su valor es 8.8542x10^-12 C²/Nm².
La unidad por carga eléctrica en el SI es el Coulomb.
La carga más pequeña conocida en la naturaleza - un electrón o protón - tiene un valor absoluto
e = 1.60219x10^-19 C.
Así, una carga con 1 Coulomb es aproximadamente igual a 6.24x10¹⁸ (= 1C/e) electrones o protones.
Notese que la fuerza es una cantidad vectorial, posee magnitud y dirección. Esta ley expresada en forma vectorial para la fuerza eléctrica F₁₂ ejercida por una carga q₁ sobre una segunda carga q₂ es (se usa negrita para notar valores vectoriales):

Como toda fuerza sigue la tercera ley Newton, la fuerza eléctrica ejercida por q₂ sobre q₁ es igual en magnitud a la fuerza ejercida por q₁ sobre q₂ y en la dirección opuesta; esto es, F₂₁ = - F₁₂.
Si q₁ y q₂ tienen el mismo signo F₁₂ toma la dirección r. Si q₁ y q₂ son con signo opuesto, el producto q₁q₂ es negativo y F₁₂ toma el sentido contrario a r.
Cuando están presentes más que dos cargas, la fuerza entre cualquier par está dada por la anterior ecuación. Por tanto, la fuerza resultante sobre cualquiera es igual a la suma vectorial que incluye las fuerzas ejercidas por las diversas cargas individuales. Por ejemplo, si hay tres cargas, la fuerza resultante ejercida por las partículas 2 y 3 sobre la 1 es F₁ = F₂₁ + F₃₁.

                         Ejercicios Ley De Coulomb

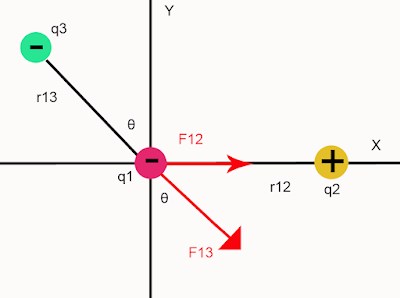
La siguiente figura muestra tres partículas cargadas:
¿Qué fuerza electrostática, debida a las otras dos cargas, actúa sobre q1?
Considere que:

q1= -1.2 μC
q2= 3.7 μC
q3= -2.7 μC
r12= 15 cm
r13= 10 cm
θ= 32°


Recordemos que μ (micro) significa 10 elevado a la menos 6
o sea que -1.2 μC es igual a -1.2x10^-6 C


Por la Ley de Coulomb sabemos que la fuerza que va a ejercer la carga q2 sobre q1 es igual a:
F12= K (q1q2)/(r12)²
donde la constante k= 9x10⁹ Nm²/C²
F12= 1.776 N


Ahora calculamos la fuerza que ejerce la carga q3 sobre la carga q1:


F13= K(q1q3)/r13
F13= 2.484 N


Nota: Al realizar los cálculos de la fuerza, no tomamos en cuenta el signo de las cargas, ya que por ahora sólo nos interesa la magnitud de dicha fuerza.


Ahora vamos a descomponer los vectores obtenidos (F12 y F13) en sus correspondientes componentes rectangulares:




La componente en x de F12 es igual a la magnitud de la fuerza que obtuvimos anteriormente, es decir Fx12= 1.77 N
Y la componente F13x= F13 sen 32°


Fx= Fx12 + Fx13= 3.09 N


Ahora obtenemos las componentes en Y:


Fy= F12y + F 13y


La componente en y de F12= 0


Fy= 0 + (-F13 cos 32°)
Fy= -2.10 N
la fuerza resulta negativa porque la carga q1 y q3 tienen el mismo signo
por lo tanto se repelen.


La fuerza total ejercida por las cargas q2 y q3 sobre q1 se obtiene:
F= √(3.09²)+(- 2.10²)
F= 3.74 N